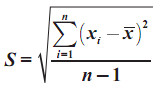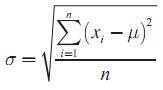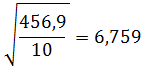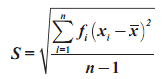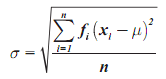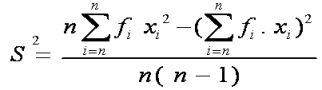BAB 5
MOMEN KEMIRINGAN DAN KURTOSIS
Ukuran Kemiringan (skewness)
Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis, yaitu :
Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar disatu
titik)
Miring ke kanan : mempunyai nilai modus paling
kecil dan rata-rata hitung
paling besar
Miring ke kiri : mempunyai nilai modus paling
besar dan rata-rata hitung paling kecil
Kemiringan simetri (normal) kemiringan Negatif positif
Untuk mengukur derajat kecondongan suatu distribusi dinyatakan dengan koefisien kecondongan (koefisien skewness).Ada tiga metode yang bisa digunakan untuk menghitung koefisien skewness yaitu :
Rumus pearson
= 1/S (X ̅ - Mod) Atau = 3/S (X ̅ – Med)
Rumus Momen
Data tidak berkelompok
3 = 1/〖nS〗^2 ∑ ( X1 X ̅ )3
Data Berkelompok
3 = 1/〖nS〗^3 ∑f i( mi - X ̅ )3
Keterangan
3 = derajat kemiringan
x1 = nilai data ke – i
X ̅ = nilai rata-rata hitung
Fi = frrekuensi nilai ke i
M1 = nilai titik tengah kelas ke-i
S = Simpangan Baku
N = Banyaknya data
Jika 3 = 0 distribusi data simetris
3 < 0 distribusi data miring ke kiri
3 > 0 distribusi data miring ke kanan
Rumus bowley
Rumus ini menggunakan nilai kuartil :
3 = (Q_3+ Q_1- 2Q_2)/(Q_3- Q_1 )
Keterangan :
Q1 = kuartil pertama
Q2 = Kuartil Kedua
Q3 = Kuaril Ketiga
Cara menentukan kemiringannya :
Jika Q3 – Q2 = Q2 – Q1 sehingga Q3 + Q1 -2Q2 = 0 yang mengakiibatkan 3 = 0, sebaliknya jika distribusi miring maka ada dua kemungkinan yaitu Q1 = Q2 atau Q2 = Q3, dalam hal Q1 = Q2 maka 3 = 1 , dan untuk Q2 = Q3 maka 3 = -1
Ukuran kemiringan data merupakan ukuran yang menunjukan apakah penyebaran data terhadap nilai rata-ratanya bersifat simetris atau tidak. Ukuran kemiringan pada dasarnya merupakan ukuran yang menjelaskan besarnya penyimpangan data dari bentuk simetris. Suat distribusi frekuensi yang miring (tidak simetris) akan memiliki nilai mean, median dan modus yang tidak sama besar (X ̅ ≠ Md ≠ Mo) sehinggan distribusi akan memusat pada salah satu sisi yaitu sisi kanan atau sisi kiri. Hal ini yang menyebabkan bentuk kurva akan miring ke kanan atau ke kiri. Jika kurva miring ke arah kanan (ekornya memanjang ke arah kiri) disebut kemiringan positif, dan jika kurva miring ke arah kiri (ekornya memnjang ke arah kanan) disebut kemiringan negatif.
Analisis kasus :
Tabel 2.1
Cara perhitungan koefisien kecondongan dengan metode
Pearson dari data penghasilan keluarga
penghasila keluarga X f U fU Fu2
10-22 16 5 -3 -15 225
23-35 29 6 -2 -12 144
36-48 42 13 -1 -13 169
49-61 55 19 0 0 0
62-74 68 11 1 11 121
75-87 81 11 2 22 484
88-100 94 5 3 15 225
Jumlah 70 ∑ fU = 8 ∑ fU2 = 1368
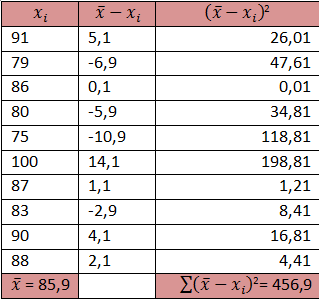
Sebelum menggunakan rumus terlebih dahulu dicari nilai , mean, median, dan standar deviasinya berikut ini:
Mean :
X ̅ = A + ((∑▒〖f.U〗)/n) . i
X ̅ = 55 + (8/70) . 3
X ̅ = 56,485
Median :
Med = Tkbmd + ((1/2 n-fkb)/fmd) . i
Med = 48.5 + ((35-24)/19) . 13
Med = 48.5 + 7,526
Med = 56,026
Standar Deviasi :
S = i √((n∑f.U^2-(∑f.U^2))/(n(n-1)))
S = 13 √(((70)-(1368)-(〖8)〗^2)/(70(70-1)))
S = 13 √19,81
S = 57,86
Setelah kita dapatkan nilai-nilai diatas, kemudian dimasukan ke dalam rumus koefisein skewness :
α = 3/S (X ̅ - Med)
α = 3/57,86 ( 56,485 – 56,026)
α = 0,0238
dari hasil perhitungan menunjukan bahwa koefisien skewness menghasilkan nilai positif, itu berarti distribusi frekuensi mempunyai bentuk kemiringan yang positif yaitu miring ke arah kanan
2.1.3 Ukuran Keruncingan (kurtosis)
Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Jika bentuk kurva runcingberarti nilai data terkonsentrasi terhadap nilai rata-tata atau nilai penyebarannya kecil, sebaliknya jika bentuk kurva nya tumpul berarti nilai data tersebar terhadap nilai rata-rata atau nilai penyebaran besar. Keruncingan distribusi data ini disebut juga kurtosis.
Derajat keruncingan suatu distribusi frekuensi dapat dibedakan menjadi tiga, yaitu:
Leptokurtis
Distribusi data yang puncaknya relatif tinggi atau bentuk distribusi yang ujungnya sangat runcing
Mesokurtis
Distribusi data yang puncaknya tidak terlalu runcing atau tidak terlalu tumpul
Platikurtis
Distribusi data yang puncaknya terlalu rendah atau terlalu mendatar
Mesokurtis leptokurtis platikurtis
Merupakan derajat atau ukuran dari ketidaksimetrisan (Asimetri) suatu distribusi data. Kemiringan distribusi data terdapat 3 jenis, yaitu :
Simetris : menunjukkan letak nilai rata-rata hitung,
median, dan modus berhimpit (berkisar disatu
titik)
Miring ke kanan : mempunyai nilai modus paling
kecil dan rata-rata hitung
paling besar
Miring ke kiri : mempunyai nilai modus paling
besar dan rata-rata hitung paling kecil
Kemiringan simetri (normal) kemiringan Negatif positif
Untuk mengukur derajat kecondongan suatu distribusi dinyatakan dengan koefisien kecondongan (koefisien skewness).Ada tiga metode yang bisa digunakan untuk menghitung koefisien skewness yaitu :
Rumus pearson
= 1/S (X ̅ - Mod) Atau = 3/S (X ̅ – Med)
Rumus Momen
Data tidak berkelompok
3 = 1/〖nS〗^2 ∑ ( X1 X ̅ )3
Data Berkelompok
3 = 1/〖nS〗^3 ∑f i( mi - X ̅ )3
Keterangan
3 = derajat kemiringan
x1 = nilai data ke – i
X ̅ = nilai rata-rata hitung
Fi = frrekuensi nilai ke i
M1 = nilai titik tengah kelas ke-i
S = Simpangan Baku
N = Banyaknya data
Jika 3 = 0 distribusi data simetris
3 < 0 distribusi data miring ke kiri
3 > 0 distribusi data miring ke kanan
Rumus bowley
Rumus ini menggunakan nilai kuartil :
3 = (Q_3+ Q_1- 2Q_2)/(Q_3- Q_1 )
Keterangan :
Q1 = kuartil pertama
Q2 = Kuartil Kedua
Q3 = Kuaril Ketiga
Cara menentukan kemiringannya :
Jika Q3 – Q2 = Q2 – Q1 sehingga Q3 + Q1 -2Q2 = 0 yang mengakiibatkan 3 = 0, sebaliknya jika distribusi miring maka ada dua kemungkinan yaitu Q1 = Q2 atau Q2 = Q3, dalam hal Q1 = Q2 maka 3 = 1 , dan untuk Q2 = Q3 maka 3 = -1
Ukuran kemiringan data merupakan ukuran yang menunjukan apakah penyebaran data terhadap nilai rata-ratanya bersifat simetris atau tidak. Ukuran kemiringan pada dasarnya merupakan ukuran yang menjelaskan besarnya penyimpangan data dari bentuk simetris. Suat distribusi frekuensi yang miring (tidak simetris) akan memiliki nilai mean, median dan modus yang tidak sama besar (X ̅ ≠ Md ≠ Mo) sehinggan distribusi akan memusat pada salah satu sisi yaitu sisi kanan atau sisi kiri. Hal ini yang menyebabkan bentuk kurva akan miring ke kanan atau ke kiri. Jika kurva miring ke arah kanan (ekornya memanjang ke arah kiri) disebut kemiringan positif, dan jika kurva miring ke arah kiri (ekornya memnjang ke arah kanan) disebut kemiringan negatif.
Analisis kasus :
Tabel 2.1
Cara perhitungan koefisien kecondongan dengan metode
Pearson dari data penghasilan keluarga
penghasila keluarga X f U fU Fu2
10-22 16 5 -3 -15 225
23-35 29 6 -2 -12 144
36-48 42 13 -1 -13 169
49-61 55 19 0 0 0
62-74 68 11 1 11 121
75-87 81 11 2 22 484
88-100 94 5 3 15 225
Jumlah 70 ∑ fU = 8 ∑ fU2 = 1368
Sebelum menggunakan rumus terlebih dahulu dicari nilai , mean, median, dan standar deviasinya berikut ini:
Mean :
X ̅ = A + ((∑▒〖f.U〗)/n) . i
X ̅ = 55 + (8/70) . 3
X ̅ = 56,485
Median :
Med = Tkbmd + ((1/2 n-fkb)/fmd) . i
Med = 48.5 + ((35-24)/19) . 13
Med = 48.5 + 7,526
Med = 56,026
Standar Deviasi :
S = i √((n∑f.U^2-(∑f.U^2))/(n(n-1)))
S = 13 √(((70)-(1368)-(〖8)〗^2)/(70(70-1)))
S = 13 √19,81
S = 57,86
Setelah kita dapatkan nilai-nilai diatas, kemudian dimasukan ke dalam rumus koefisein skewness :
α = 3/S (X ̅ - Med)
α = 3/57,86 ( 56,485 – 56,026)
α = 0,0238
dari hasil perhitungan menunjukan bahwa koefisien skewness menghasilkan nilai positif, itu berarti distribusi frekuensi mempunyai bentuk kemiringan yang positif yaitu miring ke arah kanan
2.1.3 Ukuran Keruncingan (kurtosis)
Merupakan derajat atau ukuran tinggi rendahnya puncak suatu distribusi data terhadap distribusi normalnya data. Jika bentuk kurva runcingberarti nilai data terkonsentrasi terhadap nilai rata-tata atau nilai penyebarannya kecil, sebaliknya jika bentuk kurva nya tumpul berarti nilai data tersebar terhadap nilai rata-rata atau nilai penyebaran besar. Keruncingan distribusi data ini disebut juga kurtosis.
Derajat keruncingan suatu distribusi frekuensi dapat dibedakan menjadi tiga, yaitu:
Leptokurtis
Distribusi data yang puncaknya relatif tinggi atau bentuk distribusi yang ujungnya sangat runcing
Mesokurtis
Distribusi data yang puncaknya tidak terlalu runcing atau tidak terlalu tumpul
Platikurtis
Distribusi data yang puncaknya terlalu rendah atau terlalu mendatar
Mesokurtis leptokurtis platikurtis
Derajat keruncingan distribusi data α4 dapat dihitung berdasarkan rumus berikut
Data tidak berkelompok
α4 = 1/(nS^4 ) ∑ ( Xi - X ̅)4
Data berkelompok
α4 = 1/(nS^4 ) ∑ fi ( mi - X ̅ )4
Keterangan :
α4 = Derajat keruncingan
Xi = nilai data ke – i
= nilai rata-rata hitung
fi = frekuensi kelas ke – i
mi = nilai titik tengah ke –i
S = simpangan baku
n = banyaknya data
dari penggunaan rumus diatas akan menghasilkan kemungkinan tiga nilai yaitu :
α4 = 3 distribusi keruncingan data disebut mesokurtis
α4 > 3 distribusi keruncingan data disebut leptokurtis
α4 < 3 distribusi keruncingan data disebut platikurtis
Analisis kasus :
Tabel 2.2
Cara perhitungan koofisien keruncingan
Dari data penghasilan keluarga
Penghasilan keluarga Frekuensi U f.U f.U2 f.U3 f.U4
10-22 5 -3 -15 45 -135 405
23-35 6 -2 -12 24 -48 96
36-48 13 -1 -13 13 -13 13
49-61 19 0 0 0 0 0
62-74 11 1 11 11 11 11
75-87 11 2 22 44 88 176
88-100 5 3 15 45 135 405
jumlah 70 8 182 38 1106
s = i √((n∑fU^2-(∑f.〖U)〗^2)/(n(n-1)))
s = 13 √(((70)(1368)-(〖8)〗^2)/(70(70-1)))
s = 13 √19,81
s = 57,86
Setelah kita dapatkan nilai diatas, kemudian dimasukan ke dalam rumus koefisein kurtosis :
α4 = [(∑f.U^4)/n-4{(∑f.U^3)/n}{(∑f.U^ )/n}+6{(∑f〖.U〗^2)/n} {(∑f.U)/n}^2-3{(∑f.U)/n}^4 ] i^4/s^4
α4 = [1106/70-4{38/70}{8/70}+6{182/70} {8/70}^2-3{8/70}^4 ] 〖13〗^4/〖57.86〗^4
α4 = (15.7557) (0,00255)
α4 = 0.040
Data tidak berkelompok
α4 = 1/(nS^4 ) ∑ ( Xi - X ̅)4
Data berkelompok
α4 = 1/(nS^4 ) ∑ fi ( mi - X ̅ )4
Keterangan :
α4 = Derajat keruncingan
Xi = nilai data ke – i
= nilai rata-rata hitung
fi = frekuensi kelas ke – i
mi = nilai titik tengah ke –i
S = simpangan baku
n = banyaknya data
dari penggunaan rumus diatas akan menghasilkan kemungkinan tiga nilai yaitu :
α4 = 3 distribusi keruncingan data disebut mesokurtis
α4 > 3 distribusi keruncingan data disebut leptokurtis
α4 < 3 distribusi keruncingan data disebut platikurtis
Analisis kasus :
Tabel 2.2
Cara perhitungan koofisien keruncingan
Dari data penghasilan keluarga
Penghasilan keluarga Frekuensi U f.U f.U2 f.U3 f.U4
10-22 5 -3 -15 45 -135 405
23-35 6 -2 -12 24 -48 96
36-48 13 -1 -13 13 -13 13
49-61 19 0 0 0 0 0
62-74 11 1 11 11 11 11
75-87 11 2 22 44 88 176
88-100 5 3 15 45 135 405
jumlah 70 8 182 38 1106
s = i √((n∑fU^2-(∑f.〖U)〗^2)/(n(n-1)))
s = 13 √(((70)(1368)-(〖8)〗^2)/(70(70-1)))
s = 13 √19,81
s = 57,86
Setelah kita dapatkan nilai diatas, kemudian dimasukan ke dalam rumus koefisein kurtosis :
α4 = [(∑f.U^4)/n-4{(∑f.U^3)/n}{(∑f.U^ )/n}+6{(∑f〖.U〗^2)/n} {(∑f.U)/n}^2-3{(∑f.U)/n}^4 ] i^4/s^4
α4 = [1106/70-4{38/70}{8/70}+6{182/70} {8/70}^2-3{8/70}^4 ] 〖13〗^4/〖57.86〗^4
α4 = (15.7557) (0,00255)
α4 = 0.040